TEORÍA DE MUESTREO
1. TIPOS DE MUESTREO
2. CALCULO DEL TAMAÑO DE LA MUESTRA
1. TIPOS DE MUESTREO
Muestreo probabilístico (aleatorio): En este tipo de muestreo, todos los individuos
de la población pueden formar parte de la muestra, tienen probabilidad positiva
de formar parte de la muestra. Por lo tanto es el tipo de muestreo que
deberemos utilizar en nuestras investigaciones, por ser el riguroso y
científico.
Muestreo no probabilístico
(no aleatorio): En este tipo de muestreo, puede haber clara
influencia de la persona o personas que seleccionan la muestra o simplemente se
realiza atendiendo a razones de comodidad. Salvo en situaciones muy concretas
en la que los errores cometidos no son grandes, debido a la homogeneidad de la
población, en general no es un tipo de muestreo riguroso y científico, dado que
no todos los elementos de la población pueden formar parte de la muestra. Por
ejemplo, si hacemos una encuesta telefónica por la mañana, las personas que no
tienen teléfono o que están trabajando, no podrán formar parte de la muestra.
Muestreo aleatorio simple
En un
muestreo aleatorio simple todos los individuos tienen la misma probabilidad de
ser seleccionados. La selección de la muestra puede realizarse a través de
cualquier mecanismo probabilístico en el que todos los elementos tengan las
mismas opciones de salir. Por ejemplo uno de estos mecanismos es utilizar una
tabla de números aleatorios, o también con un ordenador generar números
aleatorios, comprendidos entre cero y uno, y multiplicarlos por el tamaño de la
población, este es el que vamos a utilizar.
Muestreo aleatorio
estratificado
Es
frecuente que cuando se realiza un estudio interese estudiar una serie de
subpoblaciones (estratos) en la población, siendo importante que en la muestra
haya representación de todos y cada uno de los estratos considerados. El
muestreo aleatorio simple no nos garantiza que tal cosa ocurra. Para evitar
esto, se saca una muestra de cada uno de los estratos.
Hay dos
conceptos básicos:
Estratificación:
El criterio a seguir en la formación de los estratos será formarlos de tal
manera que haya la máxima homogeneidad en relación a la variable a estudio
dentro de cada estrato y la máxima heterogeneidad entre los estratos.
Afijación:
Reparto del tamaño de la muestra en los diferentes estratos o subpoblaciones.
Existen varios criterios de afijación entre los que destacamos:
1.
Afijación igual: Todos los estratos tienen el mismo número de elementos en la
muestra.
2.
Afijación proporcional: Cada estrato tiene un número de elementos en la muestra
proporcional a su tamaño.
3.
Afijación Neyman: Cuando el reparto del tamaño de la muestra se hace de forma
proporcional al valor de la dispersión en cada uno de los estratos.
Muestreo aleatorio
sistemático
Es un
tipo de muestreo aleatorio simple en el que los elementos se seleccionan según
un patrón que se inicia con una elección aleatoria.
Considerando
una población de N elementos, si queremos extraer una muestra de tamaño n,
partimos de un número h=N/n, llamado coeficiente de elevación y tomamos un
número al azar a comprendido entre 1 y h que se denomina arranque u origen.
La
muestra estará formada por los elementos: a, a+h, a+2h,....a+(n-1)h.
De aqui
se deduce que un elemento poblacional no podrá aparecer más de una vez en la
muestra. La muestra será representativa de la población pero introduce algunos
sesgos cuando la población está ordenada en función de determinados criterios.
Muestreo aleatorio por
conglomerados o áreas
Mientras
que en el muestreo aleatorio estratificado cada estrato presenta cierta
homogeneidad, un conglomerado se considera una agrupación de elementos que
presentan características similares a toda la población.
Por
ejemplo, para analizar los gastos familiares o para controlar el nivel de
audiencia de los programas y cadenas de televisión, se utiliza un muestreo por
conglomerados-familias que han sido elegidas aleatoriamente.
Las
familias incluyen personas de todas las edades, muy representativas de las
mismas edades y preferencias que la totalidad de la población.
Una vez
seleccionados aleatoriamente los conglomerados, se toman todos los elementos de
cada uno para formar la muestra. En este tipo de muestreo lo que se elige al
azar no son unos cuantos elementos de la población, sino unos grupos de
elementos de la población previamente formados. Elegidos estos grupos o
"conglomerados" en un número suficiente, se pasa posteriormente a la
elección, también al azar, de los elementos que han de ser observados dentro de
cada grupo, o bien, según se desee, a la observación de todos los elementos que
componen los grupos elegidos.
Por
ejemplo, para analizar los gastos familiares o para controlar el nivel de
audiencia de los programas y cadenas de televisión, se utiliza un muestreo por
conglomerados-familias que han sido elegidas aleatoriamente. Las familias
incluyen personas de todas las edades, muy representativas de las mismas edades
y preferencias que la totalidad de la población.
Una vez
seleccionados aleatoriamente los conglomerados, se toman todos los elementos de
cada uno para formar la muestra. En este tipo de muestreo lo que se elige al
azar no son unos cuantos elementos de la población, sino unos grupos de
elementos de la población previamente formados. Elegidos estos grupos o
"conglomerados" en un número suficiente, se pasa posteriormente a la
elección, también al azar, de los elementos que han de ser observados dentro de
cada grupo, o bien, según se desee, a la observación de todos los elementos que
componen los grupos elegidos.
Muestreo no Probabilístico
Existen
otros procedimientos para seleccionar las muestras, que son menos precisos que
los citados y que resultan menos costosos. El procedimiento más utilizado es el
muestreo no probabilístico, denominado opinático consistente en que el
investigador selecciona la muestra que supone sea la más representativa,
utilizando un criterio subjetivo y en función de la investigación que se vaya a
realizar.
Con el
muestreo opinático la realización del trabajo de campo puede simplificarse
enormemente pues se puede concentrar mucho la muestra. Sin embargo, al querer
concentrar la muestra, se pueden cometer errores y sesgos debidos al
investigador y, al tratarse de un muestreo subjetivo (según las preferencias
del investigador), los resultados de la encuesta no tienen una fiabilidad
estadística exacta.
Un
muestreo no probabilístico muy utilizado hoy en día por los institutos de
opinión es el de itinerarios, consistente en facilitar al entrevistador el
perfil de las personas que tiene que entrevistar en cada uno de los itinerarios
en que se realizan las entrevistas.
El
muestreo denominado de cuotas, utiliza en sucesivos sondeos al mismo conjunto
muestral (inicialmente seleccionado de forma aleatoria) y es el empleado para
medir índices de audiencia de programas televisivos.
En
muestreo se entiende por población a la totalidad del universo que interesa
considerar, y que es necesario que esté bien definido para que se sepa en todo
momento que elementos lo componen.
No
obstante, cuando se realiza un trabajo puntual, conviene distinguir entre
población teórica: conjunto de elementos a los cuales se quieren extrapolar los
resultados, y población estudiada: conjunto de elementos accesibles en nuestro
estudio.
Censo: En
ocasiones resulta posible estudiar cada uno de los elementos que componen la
población, realizándose lo que se denomina un censo, es decir, el estudio de
todos los elementos que componen la población.
La
realización de un censo no siempre es posible, por diferentes motivos: a)
economía: el estudio de todos los elementos que componen una población, sobre
todo si esta es grande, suele ser un problema costoso en tiempo, dinero, etc.;
b) que las pruebas a las que hay que someter a los sujetos sean destructivas;
c) que la población sea infinita o tan grande que exceda las posibilidades del
investigador.
Si la
numeración de elementos, se realiza sobre la población accesible o estudiada, y
no sobre la población teórica, entonces el proceso recibe el nombre de marco o
espacio muestral.
Concepto de muestreo
El
muestreo es una herramienta de la investigación científica. Su función básica
es determinar que parte de una realidad en estudio (población o universo) debe
examinarse con la finalidad de hacer inferencias sobre dicha población. El
error que se comete debido a hecho de que se obtienen conclusiones sobre cierta
realidad a partir de la observación de sólo una parte de ella, se denomina
error de muestreo. Obtener una muestra adecuada significa lograr una versión
simplificada de la población, que reproduzca de algún modo sus rasgos básicos.
Muestra:
En todas las ocasiones en que no es posible o conveniente realizar un censo, lo
que hacemos es trabajar con una muestra, entendiendo por tal una parte
representativa de la población. Para que una muestra sea representativa, y por
lo tanto útil, debe de reflejar las similitudes y diferencias encontradas en la
población, ejemplificar las características de la misma.
Cuando
decimos que una muestra es representativa indicamos que reúne aproximadamente
las características de la población que son importantes para la investigación.
a.
Población Los estadísticos usan la palabra población para referirse no sólo a
personas si no a todos los elementos que han sido escogidos para su estudio.
b.
Muestra Los estadísticos emplean la palabra muestra para describir una porción
escogida de la población. Matemáticamente, podemos describir muestras y
poblaciones al emplear mediciones como la Media, Mediana, la moda, la
desviación estándar. Cuando éstos términos describen una muestra se denominan
estadísticas.
Una
estadística es una característica de una muestra, los estadísticos emplean
letras latinas minúsculas para denotar estadísticas y muestras.
Tipos de
muestreo Los autores proponen diferentes criterios de clasificación de los
diferentes tipos de muestreo, aunque en general pueden dividirse en dos grandes
grupos: métodos de muestreo probabilísticos y métodos de muestreo no
probabilísticos.
Terminología
•
Población objeto: conjunto de individuos de los que se quiere obtener una
información.
•
Unidades de muestreo: número de elementos de la población, no solapados, que se
van a estudiar. Todo miembro de la población pertenecerá a una y sólo una
unidad de muestreo.
•
Unidades de análisis: objeto o individuo del que hay que obtener la
información.
• Marco muestral:
lista de unidades o elementos de muestreo.
•
Muestra: conjunto de unidades o elementos de análisis sacados del marco
2. CALCULO DEL TAMAÑO DE LA MUESTRA
POBLACIÓN.- Llamado también universo o colectivo, es el conjunto de todos
los elementos que tienen una característica común. Una población puede ser
finita o infinita. Es población
finita cuando está
delimitada y conocemos el número que la integran, así por ejemplo: Estudiantes
de la Universidad CUN. Es población infinita cuando a pesar de estar delimitada en
el espacio, no se conoce el número de elementos que la integran, así por
ejemplo: Todos los profesionales universitarios que están ejerciendo su
carrera.
MUESTRA.- La muestra es un subconjunto de la
población. Ejemplo: Estudiantes de 2do Semestre de la Universidad CUN.
Sus principales características son:
Representativa.- Se refiere a que todos y cada uno de los
elementos de la población tengan la misma oportunidad de ser tomados en cuenta
para formar dicha muestra.
Adecuada y
válida.- Se
refiere a que la muestra debe ser obtenida de tal manera que permita establecer
un mínimo de error posible respecto de la población.
Para que una muestra sea fiable, es
necesario que su tamaño sea obtenido mediante procesos matemáticos que
eliminen la incidencia del error.
ELEMENTO O
INDIVIDUO
Unidad mínima que compone una población.
El elemento puede ser una entidad simple (una persona)
o una entidad compleja (una familia),
y se denomina unidad investigativa.
FÓRMULA PARA CALCULAR EL TAMAÑO DE LA MUESTRA
Para calcular el tamaño de la muestra suele utilizarse la siguiente fórmula:
Donde:
n = el tamaño de la muestra.
N = tamaño de la población.
Z = Valor obtenido mediante niveles de confianza. Es un valor constante que, si no se tiene su valor, se lo toma en relación al 95% de confianza equivale a 1,96 (como más usual) o en relación al 99% de confianza equivale 2,58, valor que queda a criterio del investigador.
e = Límite aceptable de error muestral que, generalmente cuando no se tiene su valor, suele utilizarse un valor que varía entre el 1% (0,01) y 9% (0,09), valor que queda a criterio del encuestador.
La fórmula del tamaño de la muestra se obtiene de la fórmula para calcular la estimación del intervalo de confianza para la media, la cual es:
De donde el error es:
De esta fórmula del error de la estimación del intervalo de confianza para la media se despeja la n, para lo cual se sigue el siguiente proceso:
Elevando al cuadrado a ambos miembros de la fórmula se obtiene:
Multiplicando fracciones:
Eliminando denominadores:
Eliminando paréntesis:
Transponiendo n a la izquierda:
Factor común de n:
Despejando n:
Ordenando se obtiene la fórmula para calcular el tamaño de la muestra:
VÍDEO:
MAPA MENTAL
EJERCICIO
En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección A, 150 en la B, 150 en la C y 100 en la D.
 , su función de distribución,
, su función de distribución, 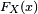 , es
, es
 . Donde en la fórmula anterior:
. Donde en la fórmula anterior: , es la probabilidad definida sobre un espacio de probabilidad y una medida unitaria sobre el espacio muestral
, es la probabilidad definida sobre un espacio de probabilidad y una medida unitaria sobre el espacio muestral 
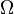 es el espacio muestral, o conjunto de todos los posibles sucesos aleatorios, sobre el que se define el espacio de probabilidad en cuestión.
es el espacio muestral, o conjunto de todos los posibles sucesos aleatorios, sobre el que se define el espacio de probabilidad en cuestión. es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.
es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.
 y
y  tal que
tal que  , los sucesos
, los sucesos  y
y  son mutuamente excluyentes y su unión es el suceso
son mutuamente excluyentes y su unión es el suceso  , por lo que tenemos entonces que:
, por lo que tenemos entonces que: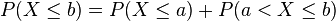


 para todos los valores de la variable aleatoria
para todos los valores de la variable aleatoria  conoceremos completamente la distribución de probabilidad de la variable.
conoceremos completamente la distribución de probabilidad de la variable.

 hasta el valor
hasta el valor 
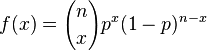

 las
las  en
en  (
(
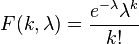



![\Phi(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x}{\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R},](https://upload.wikimedia.org/math/6/b/3/6b35a677ce8119b1eea63d02aaf3a9a3.png)
![\Phi_{\mu,\sigma^2}(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x-\mu}{\sigma\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R}.](https://upload.wikimedia.org/math/b/b/3/bb3ea66d01a7b6106216b79f48a859ba.png)
 , se denota con frecuencia
, se denota con frecuencia 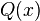 , y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.
, y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería. .
.
