DISTRIBUCIONES DE PROBABILIDAD
- PARA VARIABLES DISCRETAS
1. DISTRIBUCIÓN BINOMIAL
2. DISTRIBUCIÓN DE POISSON
- PARA VARIABLES CONTINUAS
1. DISTRIBUCIÓN NORMAL
DISTRIBUCIONES DE PROBABILIDAD
En teoría de la probabilidad y estadística,
la distribución de probabilidad de
una variable aleatoria es una función que asigna a cada suceso definido sobre
la variable aleatoria la probabilidad de
que dicho suceso ocurra. La distribución de probabilidad está definida sobre el
conjunto de todos los sucesos, cada uno de los sucesos es el rango de valores
de la variable aleatoria.
La distribución de probabilidad está completamente
especificada por la función de distribución, cuyo valor en
cada x real es la probabilidad de que la variable aleatoria sea
menor o igual que x.
Dada una variables aleatoria  , su función de distribución,
, su función de distribución, 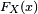 , es
, es
 , su función de distribución,
, su función de distribución, 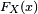 , es
, es
Por simplicidad, cuando no hay lugar a confusión, suele omitirse el subíndice  y se escribe, simplemente,
y se escribe, simplemente,  . Donde en la fórmula anterior:
. Donde en la fórmula anterior:
 y se escribe, simplemente,
y se escribe, simplemente,  . Donde en la fórmula anterior:
. Donde en la fórmula anterior: , es la probabilidad definida sobre un espacio de probabilidad y una medida unitaria sobre el espacio muestral
, es la probabilidad definida sobre un espacio de probabilidad y una medida unitaria sobre el espacio muestral  es la medida sobre la σ-álgebra de conjuntos asociada al espacio de probabilidad.
es la medida sobre la σ-álgebra de conjuntos asociada al espacio de probabilidad.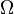 es el espacio muestral, o conjunto de todos los posibles sucesos aleatorios, sobre el que se define el espacio de probabilidad en cuestión.
es el espacio muestral, o conjunto de todos los posibles sucesos aleatorios, sobre el que se define el espacio de probabilidad en cuestión. es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.
es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.
PROPIEDADES
Como consecuencia casi inmediata de la definición, la función de distribución:
- Es una función continua por la derecha.
- Es una función monotona no decresiente.
Además, cumple
Para dos numeros reales cualesquiera  y
y  tal que
tal que  , los sucesos
, los sucesos  y
y  son mutuamente excluyentes y su unión es el suceso
son mutuamente excluyentes y su unión es el suceso  , por lo que tenemos entonces que:
, por lo que tenemos entonces que:
 y
y  tal que
tal que  , los sucesos
, los sucesos  y
y  son mutuamente excluyentes y su unión es el suceso
son mutuamente excluyentes y su unión es el suceso  , por lo que tenemos entonces que:
, por lo que tenemos entonces que:
y finalmente
Por lo tanto una vez conocida la función de distribución  para todos los valores de la variable aleatoria
para todos los valores de la variable aleatoria  conoceremos completamente la distribución de probabilidad de la variable.
conoceremos completamente la distribución de probabilidad de la variable.
 para todos los valores de la variable aleatoria
para todos los valores de la variable aleatoria  conoceremos completamente la distribución de probabilidad de la variable.
conoceremos completamente la distribución de probabilidad de la variable.
Para realizar cálculos es más cómodo conocer la distribución de probabilidad, y sin embargo para ver una representación gráfica de la probabilidad es más práctico el uso de la función de densidad .
VARIABLES DISCRETAS
Se denomina distribución de variable discreta a aquella cuya función de probabilidad sólo toma valores positivos en un conjunto de valores de  finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
 finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde  hasta el valor
hasta el valor  .
.
 hasta el valor
hasta el valor  .
.
DISTRIBUCIÓN BINOMIAL
En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
La distribución binomial es la base del test binomial de significación estadistica
EJEMPLOS
- Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:Se lanza un dado diez veces y se cuenta el número X de tres obtenidos: entonces X ~ B(10, 1/6)
- Se lanza una moneda dos veces y se cuenta el número X de caras obtenidas: entonces X ~ B(2, 1/2)
CARACTERÍSTICAS ANALÍTICAS
Su funcion de probabilidad es
donde 

siendo  las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)
 las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)Ejemplo
Supongamos que se lanza un dado (con 6 caras) 51 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(51, 1/6) y la probabilidad sería P(X=20):
En teoría de la probabilidad y estadística,
la distribución de Poisson es
una distribución de probabilidad discreta que expresa, a partir de una
frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado
número de eventos durante cierto período de tiempo. Concreta mente, se
especializa en la probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas, o sucesos "raros".
Fue descubierta por Simeon-Denis Poisson, que la dio a conocer en 1838 en su
trabajo Recherches sur la probabilité des jugements en matières
criminelles et matière civile (Investigación sobre la probabilidad
de los juicios en materias criminales y civiles).
La función de masa o probabilidad de la
distribución de Poisson es
donde
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
- e es la base de los logaritmos naturales (e = 2,71828...)
Tanto el valor esperado como la varianza de
una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden
superior son polinomio de Touchard en λ cuyos
coeficientes tienen una interpretación combinatoria De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces
según la fórmula de Dobinski,
el n-ésimo momento iguala al número de particiones de tamañon.
La moda de una variable aleatoria de
distribución de Poisson con un λ no entero es igual a ,
el mayor de los enteros menores que λ (los símbolos  representan
la función parte entera). Cuando λ es un
entero positivo, las modas son λ y λ − 1.
representan
la función parte entera). Cuando λ es un
entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de
la distribución de Poisson con valor esperado λ es
Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ0 a otra de parámetro λ es
DISTRIBUCION NORMAL
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido comométodo correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
- caracteres morfológicos de individuos como la estatura;
- caracteres fisiológicos como el efecto de un fármaco;
- caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
- caracteres psicológicos como el cociente intelectual;
- nivel de ruido en telecomunicaciones;
- errores cometidos al medir ciertas magnitudes;
- etc.
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal. Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una "normalidad" más o menos justificada de la variable aleatoria bajo estudio.
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.
La función de distribución de la distribución normal está definida como sigue:
Por tanto, la función de distribución de la normal estándar es:
Esta función de distribución puede expresarse en términos de una función especial llamada función error de la siguiente forma:
y la propia función de distribución puede, por consiguiente, expresarse así:
El complemento de la función de distribución de la normal estándar,  , se denota con frecuencia
, se denota con frecuencia 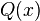 , y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.5 6 Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas ellas transformaciones simples de
, y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.5 6 Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas ellas transformaciones simples de  .7
.7
 , se denota con frecuencia
, se denota con frecuencia 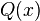 , y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.5 6 Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas ellas transformaciones simples de
, y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.5 6 Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas ellas transformaciones simples de  .7
.7
La inversa de la función de distribución de la normal estándar puede expresarse en términos de la inversa de la función de error:
y la inversa de la función de distribución puede, por consiguiente, expresarse como:
Esta función cuantil se llama a veces la función probit. No hay una primitiva elemental para la función probit. Esto no quiere decir meramente que no se conoce, sino que se ha probado la inexistencia de tal función. Existen varios métodos exactos para aproximar la función cuantil mediante la distribución normal.
Los valores Φ(x) pueden aproximarse con mucha precisión por distintos métodos, tales como integración numérica, series de Taylor, series asintóticas y fracciones continuas.
VIDEO
MAPA MENTAL
EJERCICIO
Sea X una variable aleatoria discreta cuya función de probabilidad es:
| x | p i |
|---|---|
| 0 | 0,1 |
| 1 | 0,2 |
| 2 | 0,1 |
| 3 | 0,4 |
| 4 | 0,1 |
| 5 | 0,1 |


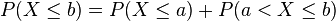




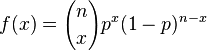

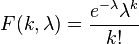



![\Phi(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x}{\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R},](https://upload.wikimedia.org/math/6/b/3/6b35a677ce8119b1eea63d02aaf3a9a3.png)
![\Phi_{\mu,\sigma^2}(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x-\mu}{\sigma\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R}.](https://upload.wikimedia.org/math/b/b/3/bb3ea66d01a7b6106216b79f48a859ba.png)


No hay comentarios:
Publicar un comentario