NOCIONES BÁSICAS DE PROBABILIDAD
1. DEFINICIÓN CLÁSICA DE PROBABILIDAD
2. CÁLCULOS DE PROBABILIDADES DE SUCESOS SIMPLES
3. CÁLCULOS DE PROBABILIDADES DE SUCESOS COMPUESTOS
4. TÉCNICAS DE CONTEO
5. TEOREMA DE BAYES
1. DEFINICIÓN CLÁSICA DE PROBABILIDAD
Esta definición clásica de probabilidad fue una de las primeras que se dieron (1900) y se atribuye a Laplace; también se conoce con el nombre de probabilidad a priori pues, para calcularla, es necesario conocer, antes de realizar el experimento aleatorio, el espacio muestral y el número de resultados o sucesos elementales que entran a formar parte del suceso.
La aplicación de la definición clásica de probabilidad puede presentar dificultades de aplicación cuando el espacio muestral es infinito o cuando los posibles resultados de un experimento no son equiprobables. Ej: En un proceso de fabricación de piezas puede haber algunas defectuosas y si queremos determinar la probabilidad de que una pieza sea defectuosa no podemos utilizar la definición clásica pues necesitaríamos conocer previamente el resultado del proceso de fabricación.
Para resolver estos casos, se hace una extensión de la definición de probabilidad, de manera que se pueda aplicar con menos restricciones, llegando así a la definición frecuentista de probabilidad.
EJEMPLO 1
Se realiza el lanzamiento de un dado bien hecho, determine lo siguiente:
- ¿Cuál es la probabilidad de obtener un tres?
- ¿Cuál es la probabilidad de obtener un número par?
- ¿Cuál es la probabilidad de obtener un número primo?
SOLUCIÓN:
a. Suceso T = “obtener un tres”. T= {3}. Luego, la probabilidad de obtener un tres será:
b. Suceso P = “sacar un número par”. P = {2,4,6}. Luego, la probabilidad de obtener un número par será:
c. Suceso Pr = “sacar un número primo”. Pr = {1,2,3,5}. Luego, la probabilidad de obtener un número primo será:
2. CÁLCULOS DE PROBABILIDADES DE SUCESOS SIMPLES
La posibilidad que hay de que ocurra algún evento determinado, por ejemplo, que de un recipiente con 5 pelotas verdes, 2 azules y 3 rojas obtengamos una roja es de .3, siempre debe ser un número menor o igual a uno, excepto cuando lo expresas en porcentaje.
Probabilidad simple es igual a la cantidad de formas en que un resultado específico va a suceder entre la cantidad total de posibles resultados.
Una manera, muy usada en la práctica, de denominar la probabilidad un evento simple de un espacio muestral es como probabilidad simple o marginal, la cual hace referencia a la probabilidad de un evento simple, y se denota con P(A), siendo A el evento simple en cuestión. El nombre de probabilidad marginal se debe a que esta medida se puede obtener a partir de los totales marginales de una tabla de contingencia.
EJEMPLO
Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?
Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:
P(Manzana)=10/30=1/3= 33.3% probable
Calculando igual, la probabilidad de sacar pera es:
P(Pera)=20/30=2/3= 66.7% probable
Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.
3. CÁLCULOS DE PROBABILIDADES DE SUCESOS COMPUESTOS
La probabilidad es un método por
el cual se obtiene la frecuencia de un acontecimiento determinado mediante la
realización de experimentos aleatorios, de los que se conocen todos los
resultados posibles, bajo condiciones suficientemente estables.
La probabilidad es un evento o suceso que puede ser improbable, probable o
seguro.
La teoría de la probabilidad se usa
extensamente en áreas como la estadística,
la física,
la matemática, las ciencias y
la filosofía para
sacar conclusiones sobre la probabilidad discreta de sucesos potenciales y la
mecánica subyacente discreta de sistemas complejos, por lo tanto es la rama de
las matemáticas que estudia, mide o determina
a los experimentos o fenómenos aleatorios.
¿Cuáles de
estos fenómenos son aleatorios?
a) Lanzar una moneda y observar si sale cara o
cruz.
b) Número de viajeros que suben al metro en
una estación.
c) Lanzar una piedra al vacío y medir su
aceleración.
d) Elegir un delegado de una clase de 25
alumnos.
e) Calcular el área de un círculo de radio 3.
SOLUCIÓN
Los
fenómenos a, b y d son aleatorios, ya que sabemos los posibles resultados pero
al realizar el experimento no se puede predecir cuál de ellos se dará. El
fenómeno c y e son deterministas porque se conocen las fórmulas que proporciona
la relación.
4. TÉCNICAS DE CONTEO
El principio fundamental en el proceso de contar ofrece un método general para contar el numero de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento Bpuede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a n1 x n2.
¿De cuántas maneras pueden repartirse 3 premios a un conjunto de 10 personas, suponiendo que cada persona no puede obtener más de un premio?
Aplicando el principio fundamental del conteo, tenemos 10 personas que pueden recibir el primer
premio. Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo, y
posteriormente quedarán 8 personas para el tercer premio. De ahí que el número de maneras
distintas de repartir los tres premios.
n
10 x 9 x 8 = 720
¿Cuántas placas de automóvil se pueden hacer utilizando dos letras seguidas de tres cifras? No se
admiten repeticiones.
26 x 25 x 10 x 9 x 8 = 468000
n un número entero positivo, el producto n (n-1) (n-2)...3 x 2 x 1 se llama factorial de n.
El símbolo ! se lee factorial y es el producto resultante de todos los enteros positivos de 1 a n; es decir, sea
n
5! = 5 x 4 x 3 x 2 x 1 = 120
Por definición 0! = 1
Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.
Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.
Para la
construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades,
acompañada de su probabilidad. En el final de cada rama
parcial se
constituye a su vez, un nudo del cual parten nuevas ramas,
según las posibilidades del siguiente paso, salvo si el nudo
representa un posible final del experimento (nudo final). Hay que tener en cuenta: que
la suma de probabilidades de las ramas de cada nudo ha de dar 1.
Una clase consta de seis niñas y 10 niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
1 Seleccionar tres niños.
2 Seleccionar exactamente dos niños y una niña.
3 Seleccionar exactamente dos niñas y un niño.
4 Seleccionar tres niñas.
Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1
5. TEOREMA DE BAYES
El teorema
de Bayes, en la teoría de la probabilidad, es una proposición
planteada por el filósofo inglés Thomas Bayes (1702-1761) en
1763, que
expresa la probabilidad condicional de un evento
aleatorio A dado B en términos de
la distribución de probabilidad condicional del evento B dado A y
la distribución de probabilidad marginal de
sólo A.
En términos más generales y menos matemáticos, el
teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de
A dado B con la probabilidad de B dado A. Es decir, que sabiendo la
probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría
saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene
un dolor de cabeza. Muestra este sencillo ejemplo la alta relevancia del
teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene
vinculación íntima con la comprensión de la probabilidad de aspectos causales
dados los efectos observados.
Con base en la definición de Probabilidad condicionada, obtenemos la Fórmula de Bayes, también conocida como la Regla de Bayes:
Esta fórmula nos permite calcular la probabilidad condicional  de cualquiera de los eventos
de cualquiera de los eventos 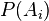 , dado
, dado  . La fórmula
. La fórmula ![[1]](https://upload.wikimedia.org/math/3/5/d/35dba5d75538a9bbe0b4da4422759a0e.png) "ha originado muchas especulaciones filosóficas y controversias".
"ha originado muchas especulaciones filosóficas y controversias".
 de cualquiera de los eventos
de cualquiera de los eventos 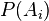 , dado
, dado  . La fórmula
. La fórmula ![[1]](https://upload.wikimedia.org/math/3/5/d/35dba5d75538a9bbe0b4da4422759a0e.png) "ha originado muchas especulaciones filosóficas y controversias".
"ha originado muchas especulaciones filosóficas y controversias".
VIDEO
MAPA MENTAL
EJERCICIO
MAPA MENTAL
EJERCICIO
Se sacan dos bolas de una urna que se compone de una bola blanca, otra roja, otra verde y otra negra. Escribir el espacio muestral cuando:



![P(A_i|B) = \frac{P(B|A_i) P(A_i)}{\sum_{k=1}^n P(B|A_k) P(A_k)}.... [1]](https://upload.wikimedia.org/math/1/4/c/14c61c0d508e0ba073b487b742a19c94.png)
No hay comentarios:
Publicar un comentario